Mander混凝土本构约束强化系数计算

何小藤2022-10-252024-02-22

前言

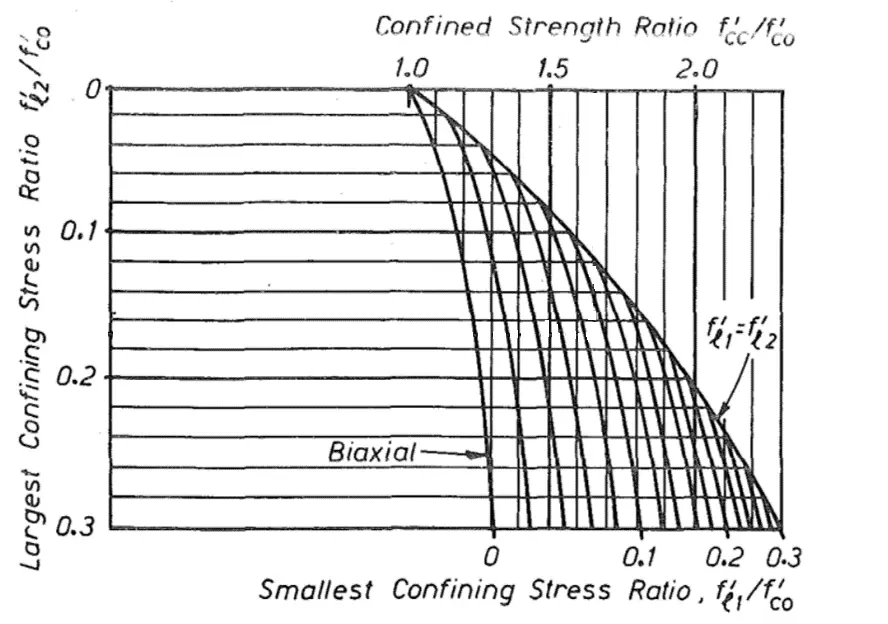
最近在整理混凝土本构关系的时候，发现Mander模型中约束混凝土强度$f_{cc}^{'}$这个参数确定十分繁琐，需要首先根据公式计算出两个方向的约束系数 $\frac{f_{lx}^{'}}{f_{c0}^{'}}$，$\frac{f_{ly}^{'}}{f_{c0}^{'}}$，然后通过查图得到约束强度系数 $\frac{f_{cc}^{'}}{f_{c0}^{'}}$，如果这个参数确定，那么就可以很容易的画出约束混凝土的应力-应变全曲线。

2022-10-25-Mander混凝土本构约束强化系数计算-1

查图不方便使用，并且精度不高，因此编写了程序“Mander混凝土本构约束强化系数计算（Mander Confined Strength Ratio）”，可以很方便的计算约束强度系数 $\frac{f_{cc}^{'}}{f_{c0}^{'}}$，并且可以导出曲线数据。

Mander本构关系计算公式

$\sigma =\frac{xrf_{cc}^{'}}{r-1+{{x}^{r}}}$ $ x=\frac{{{\varepsilon }}}{{{\varepsilon }_{cc}}}$ ${{E}_{sec}}=\frac{f_{cc}^{'}}{{{\varepsilon }_{\text{cc}}}}$ $ {{\varepsilon }_{\text{cc}}}={{\varepsilon }_{co}}\left[ 1+5\left( \frac{f_{cc}^{'}}{f_{co}^{'}}-1 \right) \right]$ ${{\varepsilon }_{co}}=0.002$ $\text{r}=\frac{{{E}_{c}}}{{{E}_{c}}-{{E}_{sec}}}>0 $

当截面的两个方向有效约束力相同时：

$\frac{f_{cc}^{'}}{f_{c}^{'}}=2.254\sqrt{1+\frac{7.94f_{l}^{'}}{f_{c}^{'}}}-2\frac{f_{l}^{'}}{f_{c}^{'}}-1.254$

对于圆形钢筋混凝土截面$f_{l}^{\prime}$的计算：

${{A}_{e}}=\frac{\pi }{4}{{\left( {{d}_{s}}-\frac{{{s}^{\prime }}}{2} \right)}^{2}}=\frac{\pi }{4}d_{s}^{2}{{\left( 1-\frac{{{s}^{\prime }}}{2{{d}_{s}}} \right)}^{2}}$ $ {{A}_{cc}}=\frac{\pi }{4}d_{s}^{2}\left( 1-{{\rho }_{cc}} \right)$ $f_{l}=\frac{1}{2} \rho_{s} f_{y h}$

体积配箍率：$\rho_{s}=\frac{4 A_{s h}}{s d_{s}}$

纵筋配筋率：$\rho_{c c}=\frac{A_{s t}}{\pi d_{s}^{2}}$

当截面的两个方向有效约束力不同时：

对于方形钢筋混凝土截面$\frac{f_{c c}^{\prime}}{f_{c}^{\prime}}$的计算：

${{f}_{lx}}=\frac{{{A}_{sx}}}{s{{d}_{c}}}{{f}_{yh}}={{\rho }_{x}}{{f}_{yh}}$ ${{f}_{ly}}=\frac{{{A}_{sy}}}{s{{b}_{c}}}{{f}_{yh}}={{\rho }_{y}}{{f}_{yh}}$ $\rho_{x}=\frac{A_{s x}}{s d_{c}}$ $\rho_{y}=\frac{A_{s y}}{s b_{c}}$ $f_{lx}^{\prime }={{k}_{e}}{{f}_{lx}}$ $f_{ly}^{\prime }={{k}_{e}}{{f}_{ly}}$ $ {{A}_{e}}=\left( {{b}_{c}}{{d}_{c}}-\sum\limits_{i=1}^{n}{\frac{{{\left( w_{i}^{\prime } \right)}^{2}}}{6}} \right)\left( 1-\frac{{{s}^{\prime }}}{2{{b}_{c}}} \right)\left( 1-\frac{{{s}^{\prime }}}{2{{d}_{c}}} \right)$ $ {{A}_{\text{cc}}}={{A}_{c}}\left( 1-{{\rho }_{cc}} \right)$ ${{A}_{\text{c}}}={{b}_{c}}{{d}_{c}}$ $k_{e}=\frac{\left(1-\sum_{i=1}^{n} \frac{\left(w_{i}^{\prime}\right)^{2}}{6 b_{c} d_{c}}\right)\left(1-\frac{s^{\prime}}{2 b_{c}}\right)\left(1-\frac{s^{\prime}}{2 d_{c}}\right)}{\left(1-\rho_{c c}\right)}$

算出$f_{lx}^{\prime }$、$f_{ly}^{\prime }$后，就可以查图得到$\frac{f_{c c}^{\prime}}{f_{c}^{\prime}}$了。

需要输入的参数

$A_{s y}$-y方向箍筋总面积
${{A}_{sx}}$-x方向箍筋总面积
$\frac{f_{cc}^{'}}{f_{c}^{'}}$-强度提高系数
$k_{e}$-有效约束系数
$f_{lx}^{\prime }$-X向有效约束系数
$f_{ly}^{\prime }$-Y向有效约束系数
$\frac{f_{lx}^{'}}{f_{c}^{'}}$-X向约束应力系数
$\frac{f_{ly}^{'}}{f_{c}^{'}}$-Y向约束应力系数
$s^{\prime }$-箍筋净距

$s$-箍筋中对中间距

${{A}_{e}}$-混凝土核心区面积（area of effectively confined concrete core）

截面宽度、截面高度、保护层厚度

${{A}_{\text{cc}}}$-箍筋所围截面面积减去该截面上纵筋的面积
${{A}_{\text{c}}}$-箍筋以内的面积（area of core of section enclosed by the center lines of the perimeter spiral or hoop）

纵筋配筋率（相对于核心区混凝土）：$\rho_{c c}=\frac{A_{s t}}{{{b}_{c}}{{d}_{c}}}$

${A_{s t}}$-纵筋总面积

参考的文献

Mander J B, Priestley M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal of structural engineering, 1988, 114(8): 1804-1826.

软件介绍

软件图标：
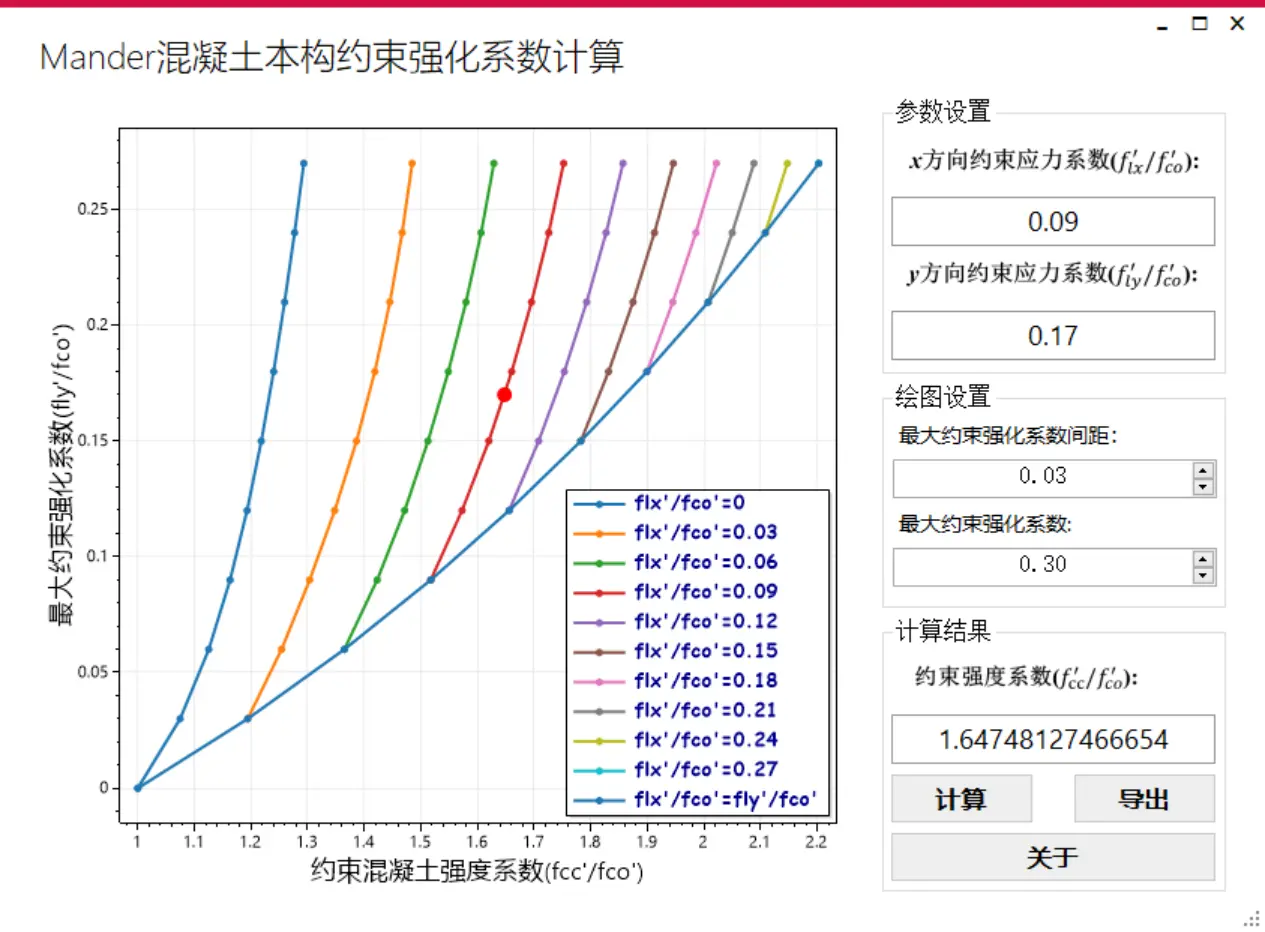
界面：

主要功能

计算混凝土本构约束强化系数
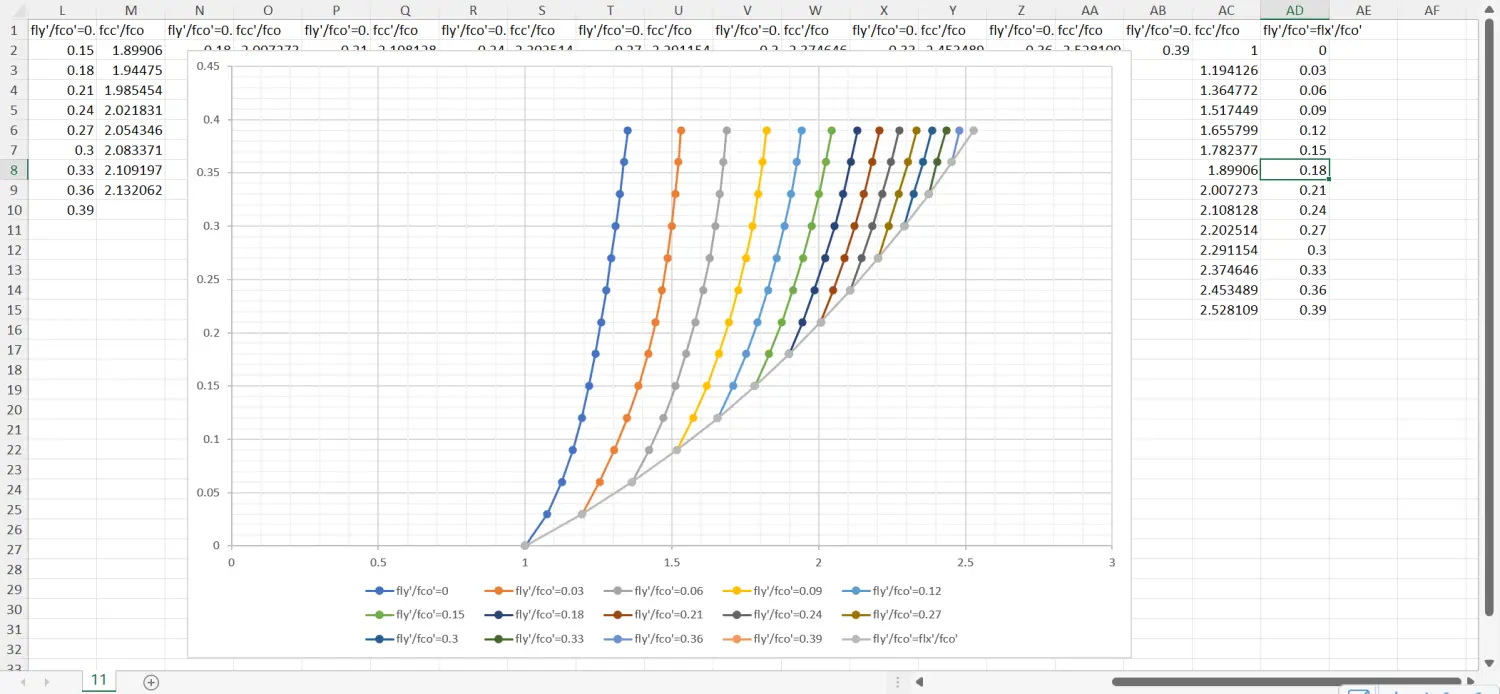
支持导出绘图数据
支持图片保存

使用教程

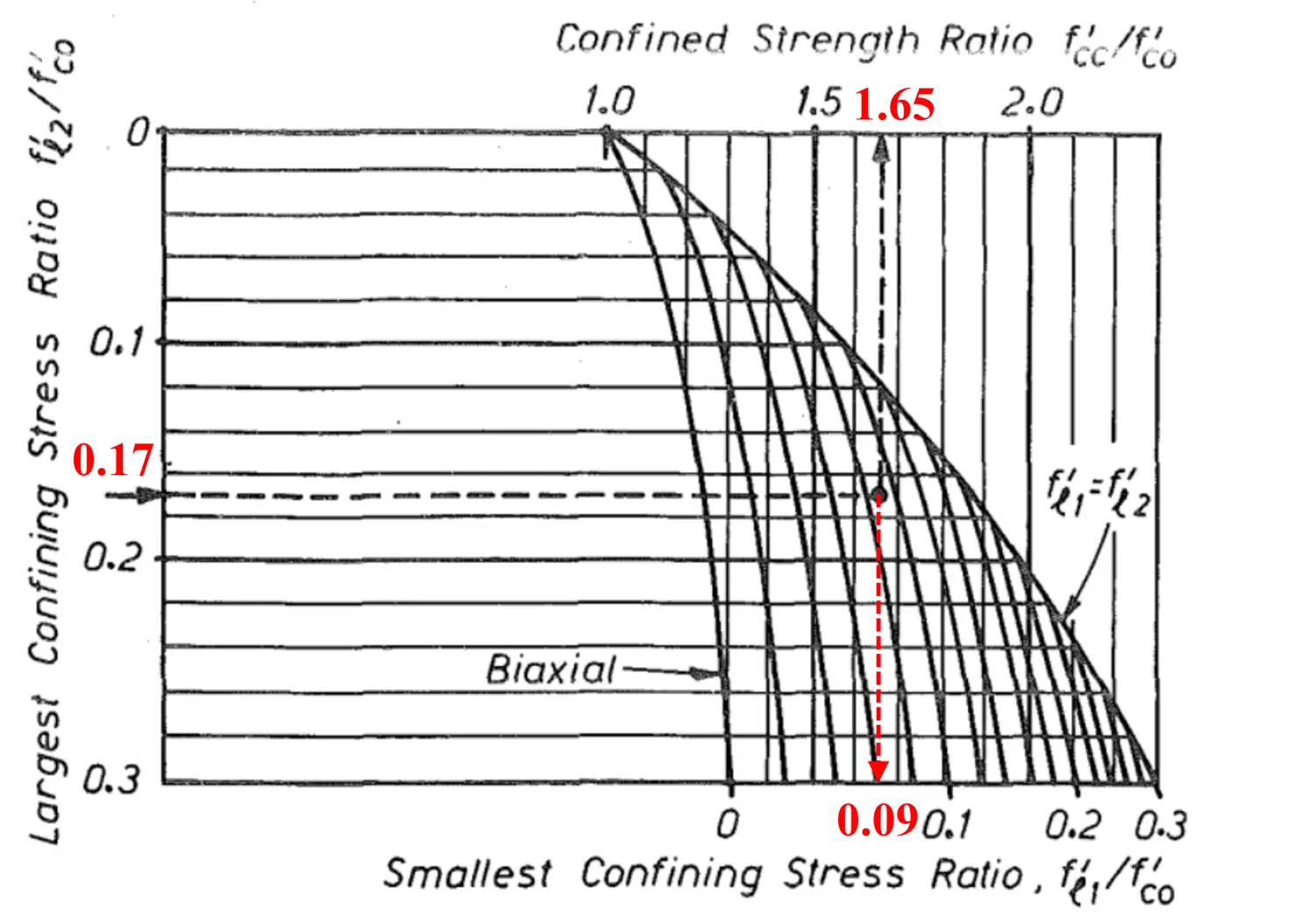
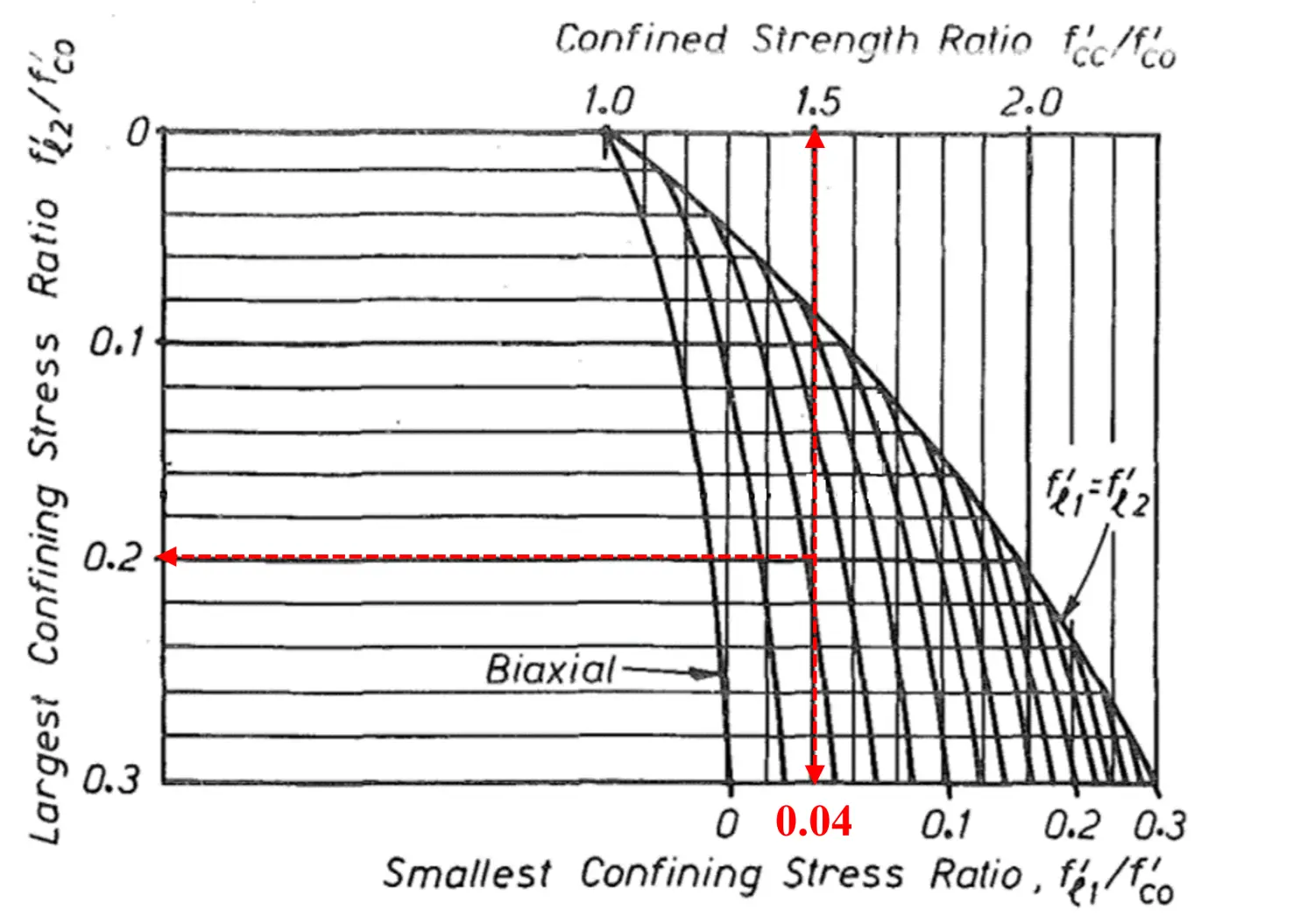
Mander原文中给出了一个计算的实例：”As a numerical example, consider a column with an unconfined strength ${f_{co}^{‘}}$= 30MPa (4350 psi) and confining stresses given by Eqs. 28 and 29 ${f_{ly}^{'}}$= 2.7 MPa (390 psi) and ${f_{lx}^{'}}$= 5.1 MPa (740 psi). Then, by following the dotted line in Fig. 4, the compressive strength of the confined concrete is found to be ${f_{cc}^{'}}$ = 1.65 x 30 = 49.5 MPa (7170psi).”
即$\frac{f_{lx}^{'}}{f_{co}^{'}}$=$\frac{5.1}{30}=0.17$，$\frac{f_{ly}^{'}}{f_{co}^{'}}$=$\frac{2.7}{30}=0.09$，查图得$\frac{f_{cc}^{'}}{f_{co}^{'}}$ = 1.65。

2022-10-25-Mander混凝土本构约束强化系数计算-5

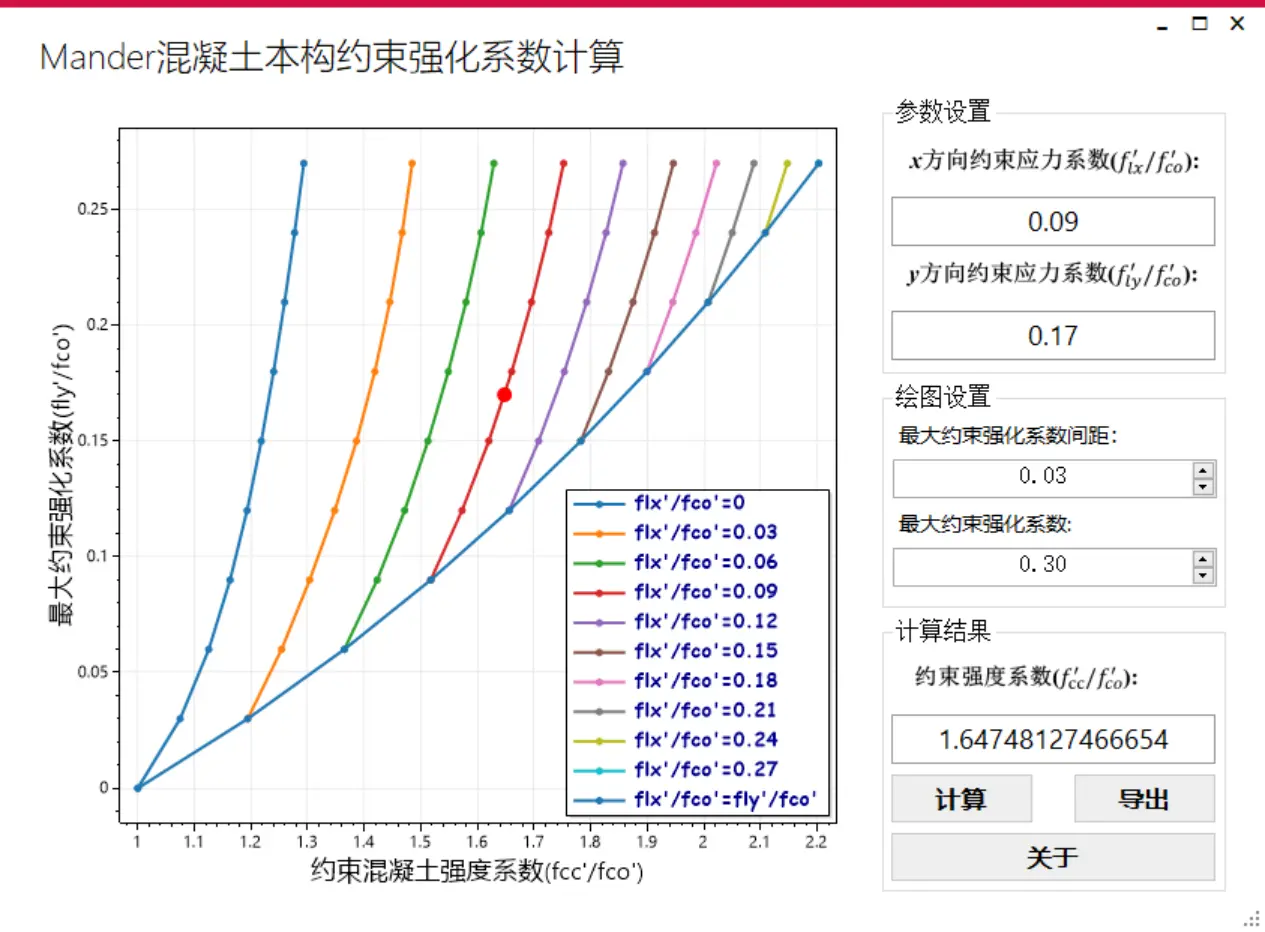
下面通过软件来计算：
2022-10-25-Mander混凝土本构约束强化系数计算-6
计算结果$\frac{f_{cc}^{'}}{f_{c0}^{'}}$ = 1.64748127466654≈1.65。

操作视频：

实例

为了说明软件计算的正确性，举几个实例。

实例1

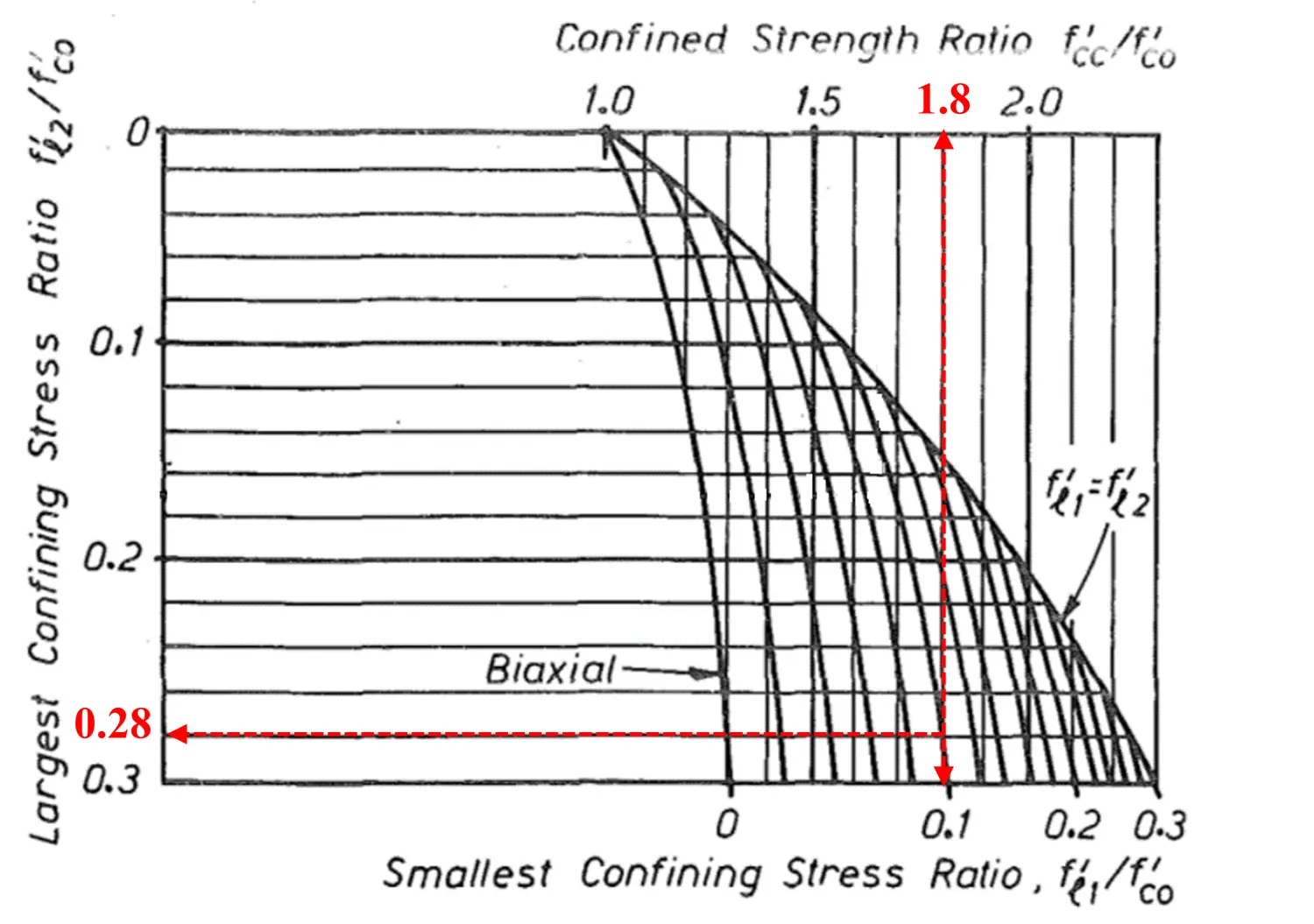
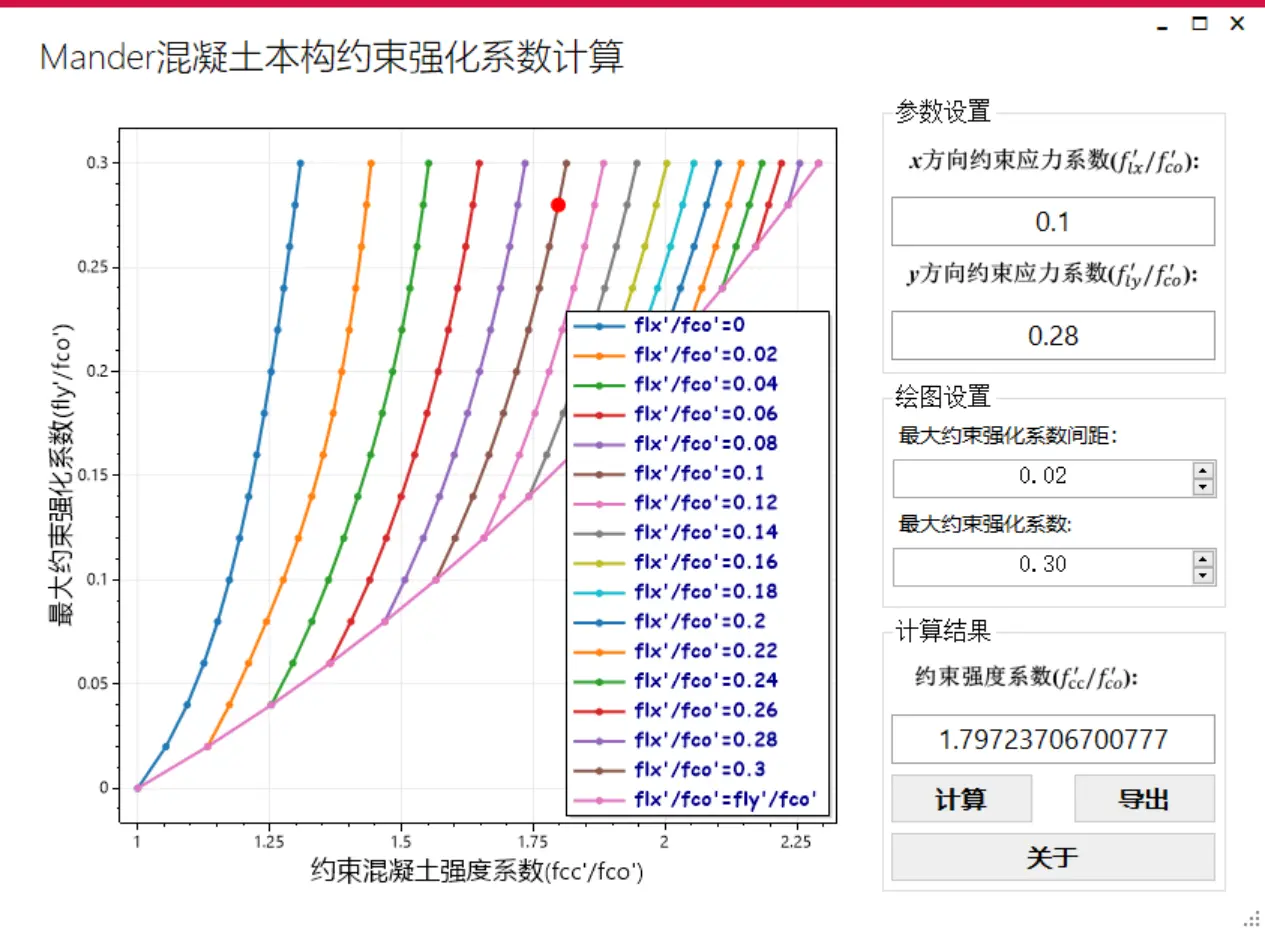
柱子非约束混凝士强度${f_{co}^{'}}$=30Mpa，两个方向的约束应力为${f_{lx}^{'}}$=3.0Mpa，${f_{ly}^{'}}$=8.4Mpa，求约束强化系数 $\frac{f_{cc}^{'}}{f_{co}^{'}}$。

计算过程：即$\frac{f_{lx}^{'}}{f_{co}^{'}}$=$\frac{3}{30}=0.1$，$\frac{f_{ly}^{'}}{f_{co}^{'}}$=$\frac{8.4}{30}=0.28$，查图得$\frac{f_{cc}^{'}}{f_{co}^{'}}$ = 1.8，软件计算结果为$\frac{f_{cc}^{'}}{f_{co}^{'}}$ =1.79723706700777≈1.8。
2022-10-25-Mander混凝土本构约束强化系数计算-8

2022-10-25-Mander混凝土本构约束强化系数计算-9

实例2

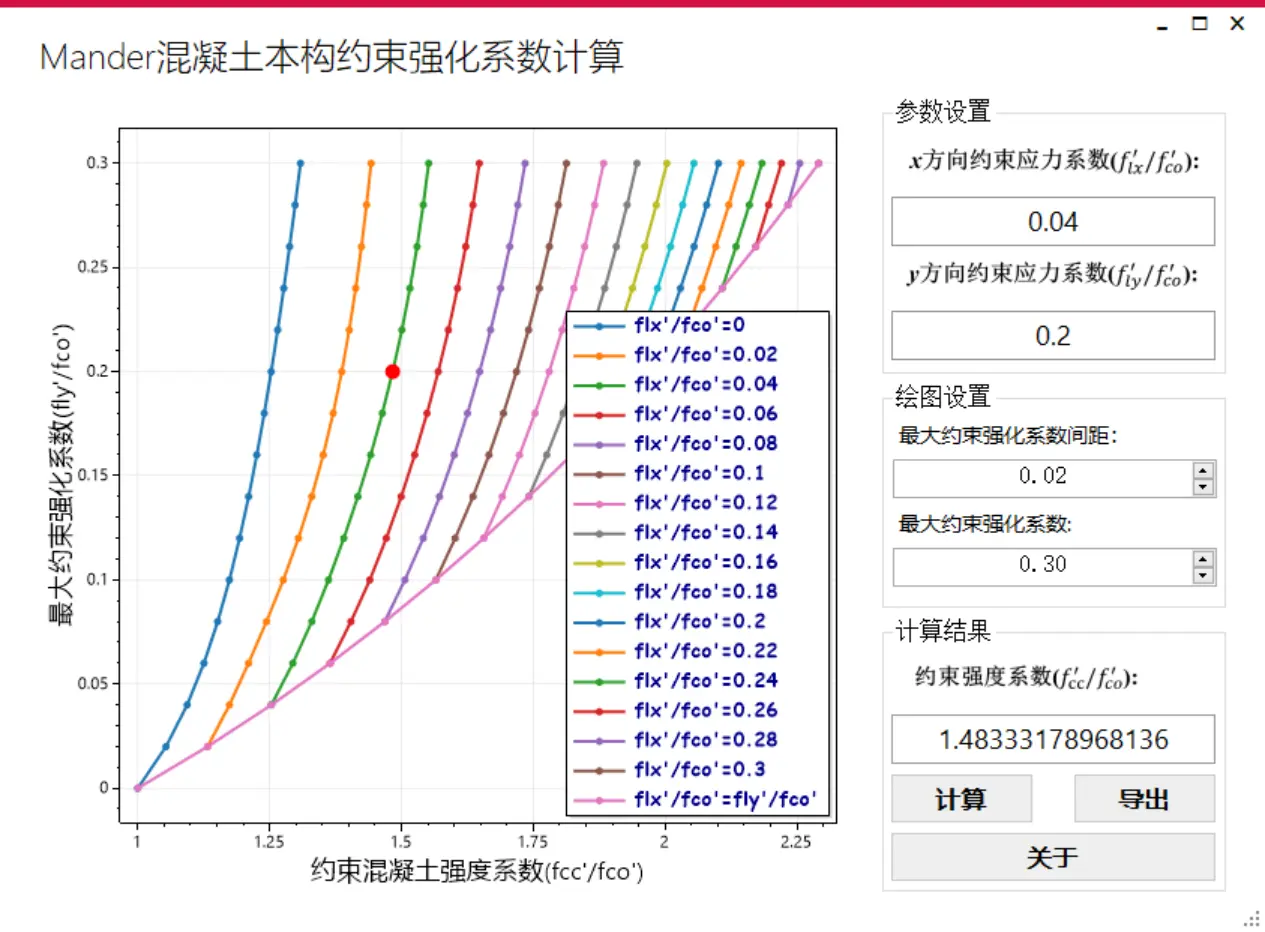
柱子非约束混凝士强度允 ${f_{co}^{'}}$=30Mpa，两个方向的约束应力为${f_{lx}^{'}}$=1.2Mpa，${f_{ly}^{'}}$=6.0Mpa，求约束强化系数 $\frac{f_{cc}^{'}}{f_{co}^{'}}$。

计算过程：即$\frac{f_{lx}^{'}}{f_{co}^{'}}$=$\frac{1.2}{30}=0.04$，$\frac{f_{ly}^{'}}{f_{co}^{'}}$=$\frac{6}{30}=0.2$，查图得$\frac{f_{cc}^{'}}{f_{co}^{'}}$ = 1.5，软件计算结果为$\frac{f_{cc}^{'}}{f_{co}^{'}}$ =1.48333178968136≈1.5。

2022-10-25-Mander混凝土本构约束强化系数计算-10